Главная

• Коллектив

• Исследования

• Публикации

• Сотрудничество

• Гранты

Контакты

Исследования

Содержание

1. Введение
2. Проблема "терагерцового провала"
3. Механизм пучково-плазменной антенны
4. Генерация узкополосного когерентного излучения в плазме под действием встречных лазерных импульсов
5. Полномасштабное моделирование экспериментов по инжекции тонкого электронного пучка в замагниченную плазму
6. Вычисление инкремента неустойчивости горячего электронного пучка в замагниченной плазме в рамках точной кинетической теории с учётом релятивистских эффектов
7. Повышение уровня электромагнитной эмиссии за счёт трёхволнового процесса слияния продольных плазменных волн в поперечную электромагнитную волну в системе с двумя встречными электронными пучками в плазме при специальным образом подобранных параметрах

Генерация узкополосного когерентного излучения в плазме под действием встречных лазерных импульсов

Как известно, плазма способна длительное время поддерживать колебания с экстремально высоким электрическим полем до десятков ГВ/см. В данный момент разрабатываются различные методики по конверсии этих осцилляций в вакуумные электромагнитные волны. Однако тот факт, что плазма непрозрачна для излучения на плазменной частоте вынуждает использовать либо градиенты плотности (что существенно увеличивает спектральную ширину излучения), либо сильные магнитные поля (что ограничивает область применения таких схем только областью низких частот излучения).

В нашей недавней работе [1] было показано, что в тонком плазменном слое возможна генерация сверхсветового возмущения за счёт рассеяния плазменной волны на продольной модуляции плотности. Также в такой системе возможен нелинейный процесс слияния первоначальной плазменной моды и рассеянных колебаний. В результате генерируется излучение на удвоенной плазменной частоте, для которого окружающая плазма прозрачна. На этом процессе и основывается рассматриваемая в данной работе схема генерации импульсов узкополосного терагерцового излучения встречными плазменными волнами [2].

Рассмотрим плазменный столб. Некий драйвер (пучок частиц или лазерный импульс) раскачивает плазменную волны, бегущую со скоростью драйвера. Сама по себе такие колебания неспособны генерировать вакуумное электромагнитное излучение. Но если в плазме имеется встречный первому драйвер, то слияние порождаемых ими плазменных волн будет иметь сверхсветовую фазовую скорость и, следовательно, сможет стать источником электромагнитных волн. В общем случае, когда драйверы имеют разную скорость, разность волновых чисел не равна нулю и генерируемое излучение направлено под углом к плазменному столбу (рисунок 1 а). В практически интересном случае релятивистских драйверов, которые имеют наибольший энергозапас, волновые числа в точности сокращаются и излучение направлено строго поперёк плазмы (рисунки 1 б и в).

Ключевым элементом предлагаемой схемы является несовпадение поперечных профилей плазменных волн. Прекрасным инструментом для их получения являются лазерные импульсы, поскольку создаваемая ими плазменная волна по ширине совпадает с шириной импульса, а она меняется по мере распространения за счёт дифракции.

Для успешной реализации предлагаемой схемы генерации излучения первостепенны следующие требования: однородная плазма и точно сведённые встречные лазерные пучки. Тоже самое необходимо и для задач лазерного кильватерного ускорения с внешней инжекцией электронов и на данный момент не представляет трудности для реализации.

Возможные схемы относительной фокусировки встречных лазерных импульсов

Первая задача которую нам надо было решить это как и куда фокусировать лазерные пучки. На рисунке показаны три различные схемы перекрытия плазменных волн, вызванные встречными импульсами 50 фс, 800 нм в плоском плазменном канале с плотностью 1,5 10¹⁸ см^-3, частота излучения примерно 22 ТГц. В верхней строке кривые σ₁(x) и σ₂(x) соответствуют характерным поперечным размерам дифрагирующих гауссовских лазерных импульсов и связывают области интенсивных лазерных амплитуд (синий для лазера 1 и оранжевый для лазера 2). Интенсивные излучающие токи локализуются в желтых перекрывающихся областях. В нижнем ряду представлены продольные профили амплитуды излучаемой волны E₀(x) для оптимальных параметров перекрытия в каждой схеме.

Лазерные импульсы можно фокусировать в одинаковые фокусные пятна, но с неким прицельным параметром (рисунок 2 схема 1).Можно фокусировать в одну точку, но в разные фокусные пятна (рисунок 2 схема 2). И, наконец, можно фокусировать в одинаковые пятна, но разнесённые на некоторое расстояние L (рисунок схема 3). Третья схема почти в 2 раза превосходит по эффективности остальные.

Линейный режим лазер-плазменного взаимодействия

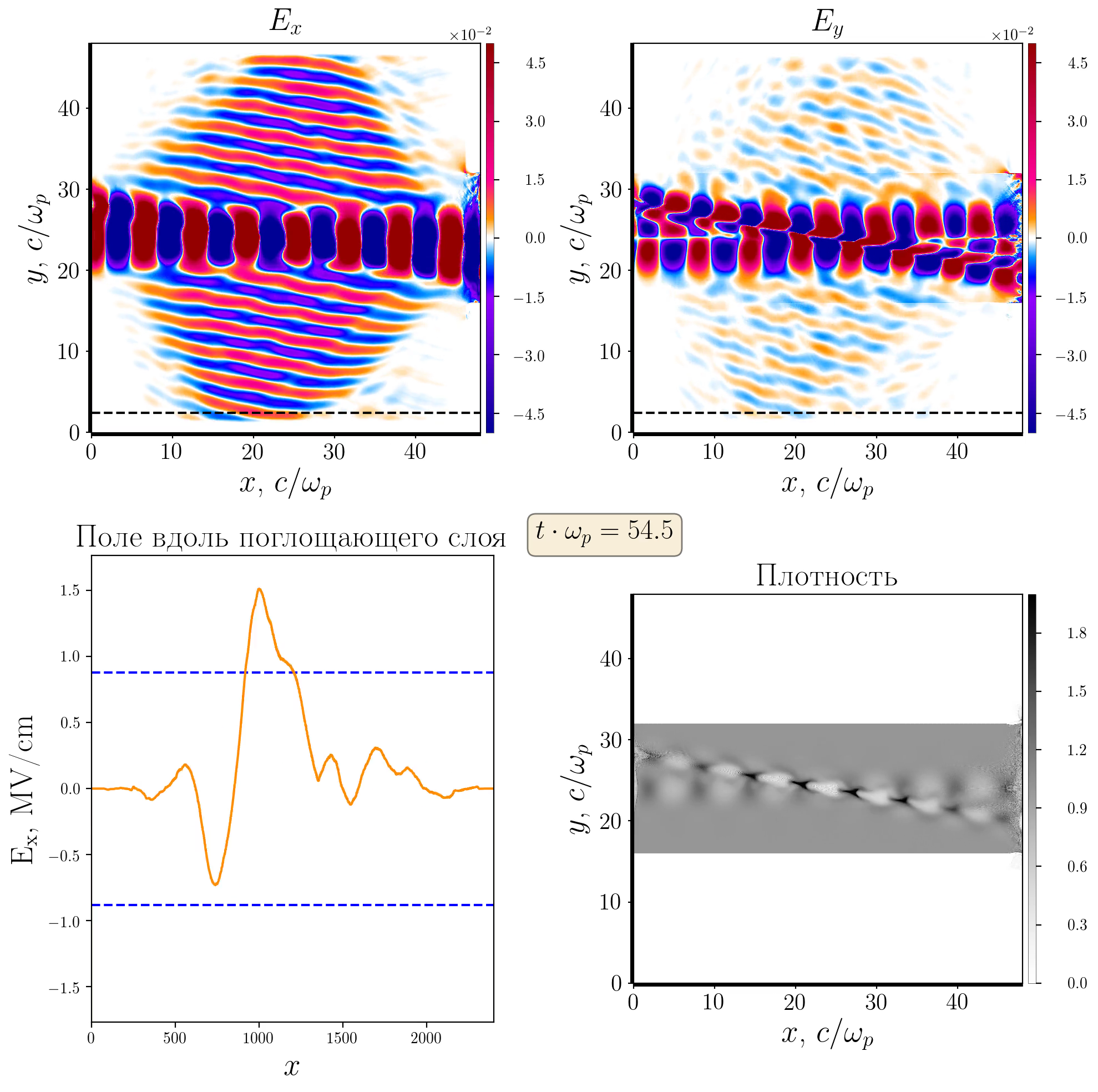
Для проверки теории (которая не учитывает затухание плазменных волн) мы рассмотрели полностью линейный случай a₀=0.4. На рисунке 2 показаны результаты моделирования. В равномерный слой плазмы с плотностью 1,5 10¹⁶ см^-3 инжектируются два лазерных импульса слева и справа. Генерируемое излучение на удвоенное плазменной частоте хорошо совпадает с теоретическим предсказанием и удерживается на этом уровне долгое время, приводя к очень узкому спектральному пику с шириной около 1%. Однако со временем эффективность генерации излучения начинает отклонятся от теоретической прямой, поскольку энергия плазменных колебаний уходит на излучение и их амплитуда снижается.

Режим вблизи нелинейного порога

Чем более мощное излучение мы хотим получить, тем более высокую амплитуду плазменных волн нам необходимо использовать. Однако чем выше амплитуда плазменных волн, тем существеннее нелинейное затухание. Для дальнейшей работы нами был выбран пограничный режим a₀=0.7, когда достигается достаточно высокая амплитуды плазменных осцилляций, однако она всё ещё хорошо совпадает с предсказаниями в рамках линейной теории. На рисунке 4 показаны результаты для такого режима. В этом случае интенсивность излучения падает гораздо быстрее. Это связано с диссипацией энергии запасённой в излучающих гармониках плазменных колебаний. Помимо потерь на излучение (7%) энергия также переходит в неизлучающие гармоники (2ω_p , ±2k) и (0, ±2k). Поэтому в дальнейших оценках мы будем предполагать a₀=0.7 и время излучения только 100ω_p^-1, хотя на самом деле излучение длится гораздо дольше и выходит на теоретический уровень через большее время.

Использование лазерных импульсов разнесённых на некоторый конечный угол

При постановке реального эксперимента велика вероятность того, что не удастся сразу точно свести встречные лазерные импульсы. Поэтому важно знать как конечный угол между лазерами влияет на излучение (и будет ли оно вообще). Теория для этого случая пока не построена, но проверить этот режим с помощью моделирования достаточно просто.

Для принципиальной проверки нами была выбрана схема 2 (рисунок 2), но при этом между лазерами был добавлен угол ~10°. На рисунке 5 показаны результаты этого моделирования. Главный вывод состоит в том, что излучение не пропало. Более подробный анализ такого режима будет проведён после построения аналитической теории.

Экспериментальная реализация

Как уже было сказано, всё что необходимо для практической реализации нашей схемы уже давно разрабатывается в контексте лазерного кильватерного ускорения. Поэтому мы можем взять готовый технические решения из это области.

Для круглых лазерных импульсов удобно использовать полые стеклянные трубки (рисунок 6а). Через трубки в боковой стенке закачивается газ, который выходит через отверстия на торце, создавая в центре трубки однородную плотность газа. Через те же торцевые отверстия в трубку вводятся лазерные импульсы. В такой системе результирующее излучение будет направлено по всей окружности.

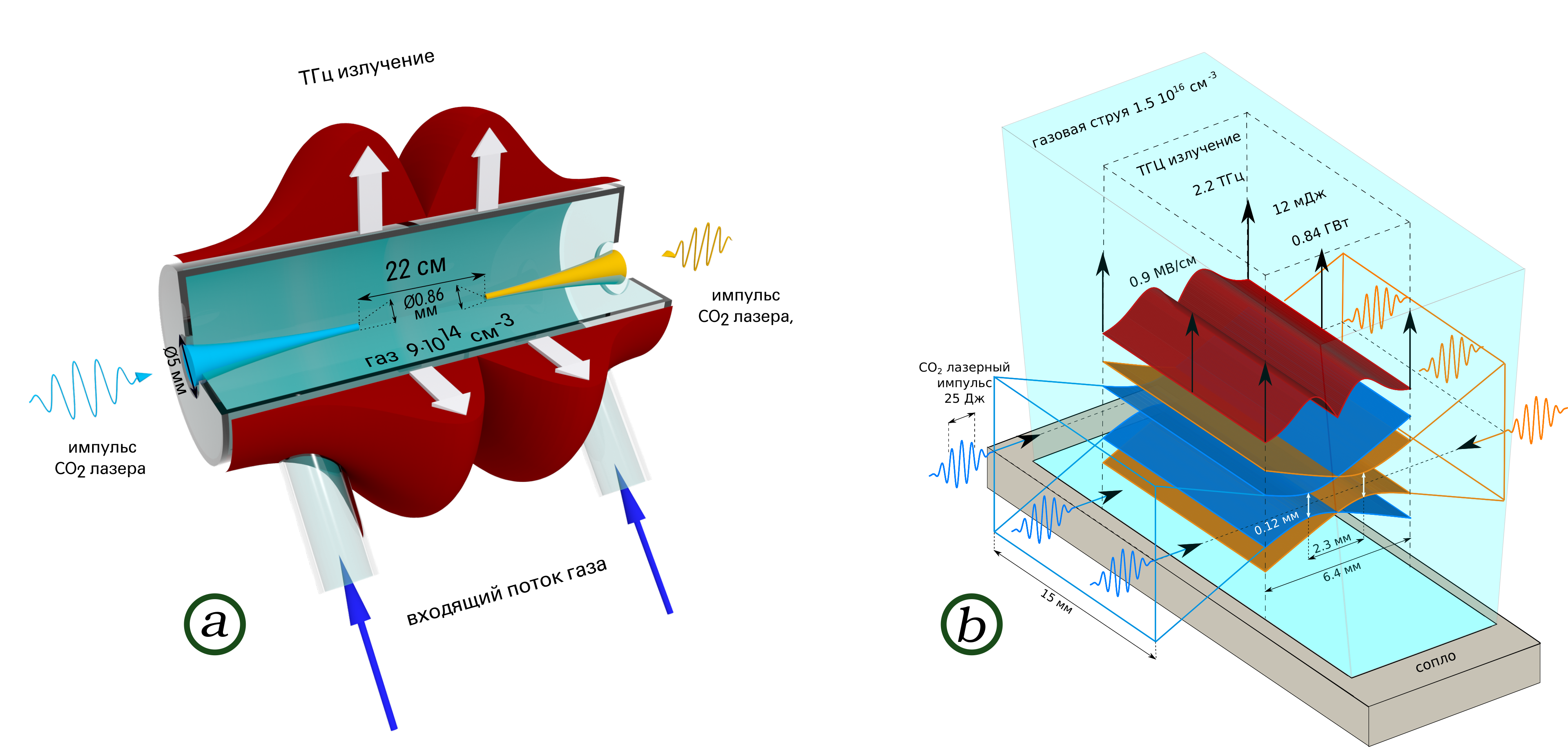
Для прямоугольных импульсов больше подходят сверхзвуковые струи газа (рисунок 6б). Такие системы выглядят более практически привлекательными, поскольку позволяют создавать направленные и протяжённые источники излучения.

В обоих случаях в качестве рабочего газа рационально использовать водород или гелий. Ввиду того, что из однородной плотности этих газов лазерные импульсы гарантированно создадут однородную плазму за счёт надбарьерной ионизации.

Генерация терагерцового излучения с помощью существующих лазерных систем

Существует длительность лазерного импульса τ~π, при которой раскачка плазменных колебаний происходит наиболее эффективно. Т.е. для каждой заданной плотности плазмы (а следовательно и излучения) существует оптимальная длительность лазерного пучка. При реализации рассматриваемой схемы для любой плотностью мы фиксируем безразмерную величину вектор-потенциала a₀=const, а также ширину лазера в фокусе σ₀=const, которая измеряется в единицах c/ω_p.

Для прямоугольных пучков, зафиксировав амплитуду и размер лазера в фокусе, возможно избыточную энергию лазера растянуть настолько, насколько её хватит. Таком образом при любой энергии превышающей некоторое значение, необходимое для создания оптимальных величин a₀ и σ₀, можно оставаться в эффективном режиме генерации излучения. Поэтому для заданной частоты необходимо подбирать только оптимальную длительность лазерного импульса (рисунок 7a).

Поскольку максимальная амплитуда излучения зависит только от амплитуды плазменных волн, а их мы фиксировали при определении величины a₀=0.7 (которая пропорциональна плазменной частоте), то величина поля излучения будет линейно расти с ростом частоты излучения (которое равняется удвоенной плазменной частоте), что показано на рисунке 7b. Эффективность раскачки плазменных волн лазерными импульсами также зависит от отношения ω_p/ω₀. это приводит к тому, что в области низких частот выгодно использовать длинноволновые CO₂ лазеры. Так с помощью 100 ТВт CO₂ лазера можно получить такое же излучение как и с использованием петаваттного ниодимого лазера (рисунок 7c).

Заключение

В рамках данной работы проводилось изучение недавно предложенного способа генерации мощных узкополосных импульсов терагерцового излучения в процессе слияния кильватерных плазменных волн, порождаемых фемтосекундными лазерными пучками гауссовской формы.

Численным моделированием подтверждено существование и эффективность данной схемы. Предложено ограничение на амплитуду используемых колебаний при котором генерируются достаточно мощные и при этом продолжительные импульсы излучения.

Осуществлена оценка параметров излучения, которого можно достичь с помощью существующих лазеров.

В дальнейшем планируется углубление теоретических знаний о такого рода системах, а также подготовка их экспериментальной проверки.

Успешная практическая реализация подобного источника излучения не только позволит выйти на новый уровень в плане генерации сверхмощных узкополосных ТГц импульсов, но и создаст возможность обеспечить большое количество лабораторий простым, компактным и эффективным источником перестраиваемого излучения, что в данный момент крайне востребовано исследователями не только в области физики, но и химии, биологии и медицины.

1. Annenkov, V. V., Volchok, E. P. & Timofeev, I. V. Generation of high-power electromagnetic radiation by a beam-driven plasma antenna. Plasma Phys. Control. Fusion 58, 45009 (2016). http://doi.org/10.1088/0741-3335/58/4/045009
2. Timofeev, I. V., Annenkov, V. V. & Volchok, E. P. (2017). Generation of high-field narrowband terahertz radiation by counterpropagating plasma wakefields. Physics of Plasmas, 24, 103106. http://doi.org/10.1063/1.4993100

Наверх

Группа теории пучково-плазменного взаимодействия, 2018