1 Пространство–время

Пространство–время — это множество всех событий. Событие характеризуется тем, что произошло где-то и когда-то. Оно однозначно определяется четырьмя числами — моментом времени и тремя пространственными координатами. То есть пространство–время четырёхмерно. Все события, произошедшие с частицей, образуют её мировую линию. В каждый момент времени частица где-то находилась, а это уже событие. Мировая линия представляет собой одномерное подмножество пространства–времени.

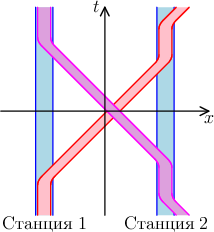
Рисовать четырёхмерные картинки довольно неудобно, поэтому мы будем в основном рассматривать движение частиц вдоль прямой. Тогда пространство–время двумерно, и его легче себе представить. Например, на рис. 1 показано движение поездов метро.

Каждый наблюдатель имеет при себе часы, и может измерять время событий на своей мировой линии. Мы примем постулат, что существуют правильно идущие часы. Показания двух правильных часов одного наблюдателя могут отличаться лишь выбором начала отсчёта (естественно, предполагается, что тиканье разных часов приведено к единой единице измерения времени). Вопрос о том, как сделать правильные часы, относится не к физике пространства–времени, а к физике населяющей его материи. Наблюдатель не может непосредственно измерить время события вне своей мировой линии. Этот процесс неизбежно включает в себя передачу сигналов, и будет подробно рассмотрен в Ї 2.

Допустим, наблюдатель 1 посылает сигнал наблюдателю 2 в момент t₁, а тот немедленно посылает сигнал обратно (рис. 2). Логически, можно представить себе три возможности:

• Возможна ситуация, когда t₂ < t₁, то есть ответный сигнал приходит раньше отправления первого сигнала. К счастью, эта возможность не соответствует нашему реальному миру; иначе про причинность можно было бы забыть.
• Разность t₂−t₁ положительна, но может быть сделана сколь угодно малой путём выбора подходящих сигналов и технических усовершенствований. В этом случае можно ввести абсолютное время, одинаковое для всех наблюдателей. Именно так все и думали до создания теории относительности.
• Разность t₂ − t₁ не может быть сделана меньше некоторого положительного значения. То есть существует наибыстрейший сигнал. Как показывают эксперименты, именно так устроен реальный мир.

Таким наибыстрейшим сигналом является свет (а также гравитационные волны). Это связано с тем, что фотоны (и гравитоны) — безмассовые частицы (Ї 5). Однако, конкретная природа наибыстрейших сигналов не является важной для теории относительности. Если когда-нибудь у фотона обнаружат очень маленькую ненулевую массу, то это будет серьёзным потрясением для теории электромагнетизма, но никак не затронет основ теории относительности. Важен только сам факт, что никакой сигнал не может быть быстрее чего-то. Мы будем для определённости называть наибыстрейшие сигналы световыми.

Пусть событие O будет взрывом бомбы. Тогда наблюдатель сначала увидит вспышку (событие A), а потом уже на него посыплются осколки (рис. 3). Мировые линии световых сигналов, испущенных в точке O, образуют световой полуконус будущего этого события. Событие O может влиять на события, лежащие внутри (и на границе) этого полуконуса, при помощи света и других сигналов (например, осколков). Эта область пространства–времени называется будущим события O.

Аналогично, мировые линии световых сигналов, приходящих в точку O, образуют световой полуконус прошлого этого события. События внутри (и на границе) этого полуконуса могут влиять на событие O. Эта область называется прошлым события O. Область пространства–времени вне светового конуса называется удалённым события O (рис. 4). События из этой области не могут влиять на O, и O не может влиять на них.

Световой конус в трёхмерном пространстве–времени (две пространственных координаты) показан на рис. 5. Будущее находится внутри светового полуконуса будущего; прошлое — внутри светового полуконуса прошлого; удалённое — вне светового конуса. В четырёхмерном пространстве–времени световой конус — это трёхмерная поверхность, нарисовать которую труднее.

2 Преобразования Лоренца

Частица, на которую не действуют никакие силы, движется по инерции. Принцип относительности Галилея гласит, что все инерциальные наблюдатели равноправны. Если один инерциальный наблюдатель поставил какой-то эксперимент и получил некоторый результат, а другой инерциальный наблюдатель поставил такой же эксперимент, то он получит такой же результат.

Допустим, два инерциальных наблюдателя пролетели мимо друг друга (событие O, рис. 6). Их часы установлены в 0 в точке O. Наблюдатель 1 послал световой сигнал в момент времени t₁ (по своим часам); наблюдатель 2 его принял в момент t₂ (по своим часам). Тогда

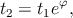(2.1)

где величина φ называется углом между мировыми линиями наблюдателей 1 и 2.

Почему эту величину естественно назвать углом? Рассмотрим трёх инерциальных наблюдателей, движущихся в одной плоскости. Пусть их мировые линии пересекаются в одной точке (O, рис. 7). Тогда

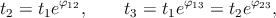откуда следует

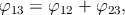(2.2)

как в обычной евклидовой геометрии. Подчеркнём ещё раз, что простой закон сложения углов (2.2) верен только для мировых линий в одной плоскости (как и в евклидовой геометрии).

Пусть теперь наблюдатель 1 посылает световой сигнал в момент t₁ (по своим часам); наблюдатель 2 получает его в момент t (событие A), и сразу посылает ответный сигнал; наблюдатель 1 получает его в момент t₂ (рис. 8). Как мы знаем, t = t₁e^φ; кроме того, t₂ = te^φ, ведь наблюдатели 1 и 2 равноправны. Значит,

(2.3)

Событие A произошло вне мировой линии наблюдателя 1, поэтому он не может непосредственно измерить время этого события по своим часам. Наиболее естественно определить время события A с точки зрения наблюдателя 1 как середину интервала [t₁,t₂], так как световой сигнал распространяется в обе стороны одинаково быстро. По той же причине, наиболее естественно определить координату события A с точки зрения наблюдателя 1 как половину этого промежутка времени. Скорость наибыстрейшего сигнала мы принимаем за 1, что фиксирует естественную единицу измерения расстояния; сигнал пропутешествовал от наблюдателя 1 до события A и обратно. Таким образом, по определению, временная и пространственная координаты события A с точки зрения наблюдателя 1 есть

(2.4)

Подставляя (2.3), получим

(2.5)

Мы пришли к очень важному результату: величина

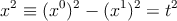(2.6)

не зависит от того, как движется наблюдатель 1 (т. е. от φ). Компоненты x⁰, x¹ вектора x (из точки O в точку A) различны для разных наблюдателей; инвариантную величину x² естественно назвать квадратом длины вектора x, т. е. квадратом расстояния от O до A. Это расстояние есть t, то есть интервал времени между событиями O и A по часам наблюдателя 2 (оба события лежат на его мировой линии). Формула (2.6) для квадрата длины вектора отличается от привычной евклидовой тем, что вместо знака + между двумя членами стоит знак −. Поэтому геометрия пространства–времени называется псевдоевклидовой (или геометрией Минковского).

Из формулы (2.5) видно, что привычная ньютоновская скорость наблюдателя 2 по отношению к наблюдателю 1 есть

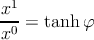(она всегда < 1, и стремится к 1 при φ →∞). Эта величина, однако, неудобна; удобнее использовать угол φ между мировыми линиями, обладающий естественным свойством аддитивности (2.2).

Как связаны координаты x⁰, x¹ события A с точки зрения наблюдателя 1 и координаты x^0′, x^1′ того же события с точки зрения наблюдателя 2, мировая линия которого образует угол φ с мировой линией наблюдателя 1? Из рис. 9 мы видим

где

(2.7)

Подставляя

мы окончательно получаем

(2.8)

Это преобразование Лоренца. Легко проверить, что квадрат длины вектора x инвариантен: (x^0′)² − (x^1′)² = (x⁰)² − (x¹)². Преобразование Лоренца проще выглядит в координатах светового фронта (приложение A).

3 Геометрия Минковского

Рассмотрим вектор x из точки O в точку A. Возможны три случая (рис. 4):

• x² > 0 — времениподобный вектор, может быть направлен в будущее или в прошлое (событие A лежит в будущем или прошлом события O). Произведя подходящее преобразование Лоренца, можно добиться того, чтобы единственной ненулевой компонентой была x⁰ (для этого достаточно провести мировую линию наблюдателя через O и A).
• x² = 0 — светоподобный вектор, направлен вдоль светового конуса в будущее или прошлое (событие A лежит на световом конусе события O). Два светоподобных вектора невозможно сравнивать (который длиннее, а который короче), за исключением случая, когда они коллинеарны.
• x² < 0 — пространственноподобный вектор (событие A лежит в удалённом события O). Произведя подходящее преобразование Лоренца, можно добиться того, чтобы единственной ненулевой компонентой была x¹ (т. е. чтобы события O и A были одновременны).

Мы знаем, что такое квадрат вектора x² (2.6). А как насчёт скалярного произведения двух векторов x ⋅ y? Его можно определить как

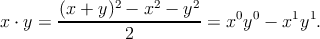В четырёхмерном пространстве–времени x⋅y = x⁰y⁰ −x¹y¹ −x²y² −x³y³. Поэтому наряду с контравариантными компонентами x^μ вектора x (μ = 0, 1, 2, 3) вводят ковариантные компоненты x_μ:

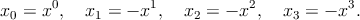Тогда скалярное произведение имеет простой вид

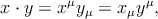(3.1)

где по повторяющемуся индексу (один раз сверху и один раз снизу) всегда подразумевается суммирование от 0 до 3.

Векторы x и y называются ортогональными, если x ⋅ y = 0. Два времениподобных вектора не могут быть ортогональны друг другу: их скалярное произведение всегда > 0, если оба направлены в будущее (или в прошлое), и < 0, если один направлен в будущее, а другой в прошлое. Светоподобный вектор ортогонален сам себе, а также всем коллинеарным с ним светоподобным векторам. Он не может быть ортогонален времениподобному вектору или светоподобному вектору, не коллинеарному с ним. Времениподобный вектор x ортогонален пространственноподобному вектору y, если их направления симметричны друг другу относительно светоподобной прямой (рис. 10): если y⁰ = x¹, y¹ = x⁰, то x ⋅ y = 0; ортогональность не нарушится, если y умножить на скаляр. Два пространственноподобных вектора могут быть ортогональны друг другу, если имеется не менее двух пространственных координат: если натянутая на них плоскость пространственноподобна, то её геометрия евклидова, и эти два вектора могут быть ортогональны.

Времениподобный вектор x длины t (x² = t²), направленный под углом φ к оси времени, имеет компоненты (2.5) x^μ = t(cosh φ, sinh φ) (рис. 11). То есть его проекция на направление e^μ = (1, 0) есть t cosh ϑ. Она всегда ≥ t; равенство достигается при φ = 0.

Скалярное произведение двух времениподобных векторов x и y (будем считать, что оба направлены в будущее) равно длине вектора x (то есть 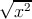), умноженной на проекцию y на направление x (она равна 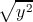cosh φ):

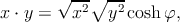(3.2)

где φ — угол между направлениями x и y. Скалярное произведение всегда ≥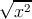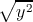; равенство достигается, когда они коллинеарны (φ = 0).

“Окружность” — это геометрическое место точек A, удалённых от центра O на расстояние t. Она определяется уравнением x² = t², и представляет собой гиперболу (рис. 12a). Она имеет две ветви, в будущем и в прошлом, представляющие собой пространственноподобные кривые; асимптотами являются образующие светового конуса. Верхнюю ветвь можно параметрически задать как

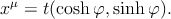(3.3)

Если же “окружность” имеет пространственноподобный радиус (x² = −r², рис. 12b), то ветви — времениподобные кривые, расположенные в области удалённого. Правая ветвь параметрически задаётся как

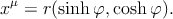(3.4)

Времениподобный вектор (3.3) ортогонален пространственноподобному вектору (3.4) с тем же φ (рис. 10).

Точки на “окружности” (3.4), соответствующие углу 0 и малому углу Δφ, разделены вектором x^μ = (rΔφ, 0) длины rΔφ (Рис. 13). Длина дуги между углами φ и φ + Δφ равна rΔφ при любом φ, потому что поворотом можно превратить угол φ в 0, а φ + Δφ в Δφ. То есть связь угла и длины дуги такая же, как в евклидовой геометрии.

В трёхмерном пространстве–времени (две пространственных координаты) “сфера” x² = t² представляет собой двухполостный гиперболоид (рис. 14a). Он состоит из двух пространственноподобных поверхностей, одна в будущем, а другая в прошлом. “Сфера” x² = −r² — однополостный гиперболоид (рис. 14b), времениподобная поверхность, лежащая в области удалённого. В четырёхмерном пространстве–времени их нарисовать сложнее.

Рассмотрим сумму двух времениподобных векторов x = OB и y = BA, направленных в будущее (рис. 15). На рисунке изображены дуги “окружностей”: расстояния от O до B и до C одинаковы, как и расстояния от A до B и до D. Очевидно, что расстояние от O до A больше, чем сумма расстояний от O до B и от B до A:

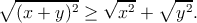(3.5)

Равенство достигается, когда x и y коллинеарны; если векторы x и y светоподобны, то 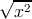+ 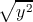= 0. Иными словами, проекция OE вектора OB на направление OA длиннее самого вектора OB (рис. 11); точно так же, проекция EA вектора BA на направление OA длиннее самого вектора BA. Это неравенство легко получить и по-другому: достаточно возвести его в квадрат и использовать (3.2).

Любую времениподобную мировую линию, соединяющую события O и A, можно сколь угодно точно приблизить ломаной. Из неравенства треугольника (3.5) следует, что прямая OA имеет наибольшую длину среди всех этих мировых линий. То есть время между O и A по часам инерциального наблюдателя больше, чем по часам любого другого наблюдателя, двигавшегося с ускорением¹.

Если у нас есть ортонормированный базис e₀, e₁, т. е. такой, что

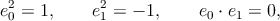(3.6)

то любой вектор x можно по нему разложить:

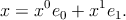(3.7)

Компоненты вектора получаются проецированием на векторы базиса:

(3.8)

(как мы уже обсуждали, x₀ = x⁰, x ₁ = −x¹).

В системе отсчёта инерциального наблюдателя 1, вектор e₀ направлен вдоль мировой линии этого наблюдателя, т. е. вдоль его оси времени: e₀^μ = (1, 0). Иными словами, это вектор скорости наблюдателя 1 (Ї 4). Вектор e₁ ему ортогонален: e₁^μ = (0, 1). Пусть имеется ещё один инерциальный наблюдатель, мировая линия которого образует угол φ с мировой линией первого наблюдателя (рис. 16). Орт оси времени второго наблюдателя e₀^′μ = (cosh φ, sinh φ) направлен из начала координат в точку на единичной окружности под углом φ. Орт оси x ортогонален ему: e₁^′μ = (sinh φ, cosh φ), и его конец лежит на окружности x² = −1. То есть орты второго наблюдателя получаются из ортов первого поворотом на угол φ:

(3.9)

Компоненты вектора x (3.7) в повёрнутой системе координат легко найти проецированием:

(3.10)

Это ни что иное как преобразование Лоренца (2.8).

4 Скорость и ускорение

Мировую линию частицы можно задать параметрически как x^μ(t). Её скорость — это вектор

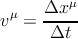(4.1)

при малом Δt, где вектор Δx^μ = x^μ(t + Δt) − x^μ(t), Δx² = Δt² (рис. 17). Поэтому

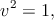(4.2)

то есть скорость v^μ(t) — это единичный касательный вектор к мировой линии в точке x^μ(t), направленный в будущее. Мировая линия частицы, движущейся по инерции, прямая:

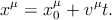(4.3)

Ускорение — это

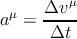(4.4)

при малом Δt. Поскольку (v + Δv)² = v² + 2v ⋅ Δv = v² = 1,

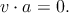(4.5)

То есть ускорение — пространственноподобный вектор, ортогональный скорости.

Пусть мировой линией частицы будет правая ветвь гиперболы

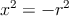(4.6)

(рис. 18). Параметрически она задаётся как x^μ = r(sinh φ, cosh φ). Длина дуги (т. е. время) для точки с углом φ есть t = rφ (если выбрать начало отсчёта времени в точке φ = 0). Поскольку (x + Δx)² = x² + 2x ⋅ Δx = x² = −r², x ⋅ v = 0, то есть скорость — времениподобный вектор, ортогональный x. При изменении t от −∞ до +∞ конец вектора x пробегает мировую линию

(4.7)

— правую ветвь гиперболы. При этом конец вектора v(t) пробегает верхнюю ветвь гиперболы v² = 1, и в каждый момент t остаётся ортогональным x(t), то есть характеризуется тем же углом φ (рис. 18). Ускорение a^μ(t) ортогонально v^μ(t), и потому направлено вдоль x^μ(t):

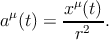(4.8)

Поэтому a² = −1∕r² постоянно; такое движение естественно назвать равноускоренным.

Рассмотрим теперь пример с двумя пространственными координатами. Протон в коллайдере равномерно движется по окружности радиуса r с периодом T₀ = 2π∕ω₀ по часам покоящегося наблюдателя. Его мировая линия — спираль (рис. 19a)

(4.9)

Если мысленно развернуть цилиндр, на который намотана спиральная мировая линия, то станет ясно, что за период протон проходит T₀ вдоль оси x⁰ и 2πr в пространственном направлении. Поэтому период движения по часам протона равен

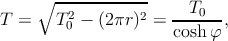(4.10)

где

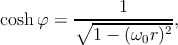(4.11)

то есть протон движется под углом φ к оси x⁰. Мировую линию можно также задать через собственное время t:

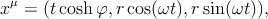(4.12)

где ω = 2π∕T = ω₀ cosh φ (энергия протона E = m cosh φ, см. Ї 5). Вектор скорости описывает конус, расположенный внутри светового конуса (Рис. 19b):

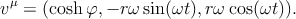(4.13)

Его конец пробегает окружность радиуса sinh ϑ = ωr, то есть длины 2πωr, за период собственного времени T = 2π∕ω. Поэтому длина вектора ускорения (пространственноподобная) равна ω²r, и

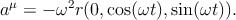(4.14)

5 Импульс и волновой вектор

Каждая частица характеризуется своей массой m. Вектор

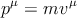(5.1)

называется импульсом. Иными словами, импульс — это касательный вектор к мировой линии длины m, направленный в будущее:

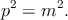(5.2)

Все возможные векторы импульса частицы образуют часть “сферы” (5.2), лежащую в будущем (рис. 14a), она называется массовой поверхностью.

Безмассовые частицы имеют светоподобный импульс: p² = 0. Например, фотон имеет m = 0. Мировые линии безмассовых частиц светоподобны. Любой интервал времени вдоль такой мировой линии равен 0; поэтому для них невозможно определить скорость. Импульс, однако, хорошо определён, и является касательным вектором к мировой линии. Массовая поверхность частицы с m = 0 — это световой полуконус будущего (рис. 5).

В системе отсчёта некоторого инерциального наблюдателя p^μ = (E,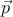 ), где временная компонента E называется энергией, а пространственные компоненты образуют трёхмерный импульс 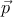. Они связаны как p² ≡ E² − 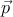² = m². То есть энергия частицы, имеющей импульс p^μ, с точки зрения наблюдателя со скоростью v^μ есть E = p ⋅ v.

Рассмотрим распад частицы с массой m на две частицы с массами m₁ и m₂. Их импульсы связаны законом сохранения

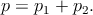(5.3)

По неравенству треугольника (3.5) m > m₁ + m₂. Какова энергия частицы 1 в системе покоя распадающейся частицы? Перепишем закон сохранения (5.3) в виде p − p₁ = p₂ и возведём в квадрат: (p − p₁)² = m² + m ₁² − 2p ⋅ p ₁ = m₂². Но p ⋅ p ₁ = mE₁, поэтому

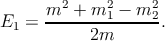(5.4)

Точно так же

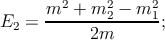(5.5)

легко проверить сохранение энергии E₁ + E₂ = m. Трёхмерные импульсы продуктов распада в системе покоя p противоположны: 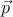₁ + 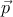₂ = 0; по модулю они равны

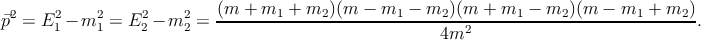(5.6)

Например, в распаде π⁰ → γγ массы фотонов m ₁ = m₂ = 0, и E₁ = E₂ = m∕2.

Ещё один пример — эффект Комптона. Фотон с энергией E рассеивается на угол ϑ на покоящемся электроне. Найдём энергию E′ рассеянного фотона. Пусть импульсы начальных электрона и фотона будут p и k, а конечных p′ и k′:

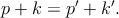(5.7)

Перепишем закон сохранения импульса в виде p + k − k′ = p′ и возведём его в квадрат: (p + k − k′)² = m² + 2p ⋅ k − 2p ⋅ k′− 2k ⋅ k′ = m². В системе покоя начального электрона p = (m,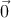), k = E(1,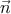), k′ = E′(1,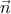′), где 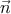, 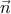′ — единичные трёхмерные векторы в направлении движения начального и конечного фотонов. Поэтому p ⋅ k = mE, p ⋅ k′ = mE′, k ⋅ k′ = EE′(1 − cos ϑ), и мы получаем

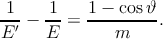(5.8)

И ещё один пример. Пион с энергией E_π налетает на покоящийся нуклон. При каких E_π может происходить реакция Nπ → ΛK (m_Λ + m_K > m_N + m_π)? Закон сохранения импульса

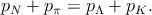(5.9)

Квадрат массы конечного состояния (p_Λ + p_K)² ≥ (m _Λ + m_K)². Перепишем его через импульсы начальных частиц: (p_N + p_π)² = m _N² + m _π² + 2m _NE_π ≥ (m_Λ + m_K)², откуда

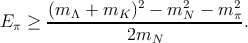(5.10)

На пороге рождающиеся Λ и K имеют одинаковые скорости, т. е. p_Λ и p_K коллинеарны.

Теперь мы рассмотрим волны. Плоская волна

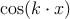(5.11)

характеризуется волновым вектором k. Если k² > 0, то можно перейти в систему покоя, где k = (k⁰,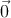). В ней волна (5.11) представляет собой колебания cos(k⁰x⁰), синхронные во всём пространстве (рис. 20a). В произвольной системе отсчёта, поверхности постоянной фазы (например, максимумы, минимумы и нули волны (5.11)) представляют собой пространственноподобные плоскости, ортогональные волновому вектору k (рис. 20b). Если k² = 0 (как для электромагнитных волн), то системы покоя не существует. В этом случае плоскости постоянной фазы светоподобны, и светоподобный вектор k лежит на такой плоскости (рис. 20c).

Наблюдатель со скоростью v имеет мировую линию x = vt. Он воспримет волну (5.11) как колебания cos(ωt) с частотой ω = k ⋅ v. Частоты волны с точки зрения разных наблюдателей различны (эффект Допплера).

A Координаты светового фронта

Иногда удобно вместо компонент x⁰, x¹ вектора x в ортонормированном базисе использовать

(A.1)

Для события A на рис. 8, x₊ = t₂ = te^φ, x ₋ = t₁ = te^−φ. Квадрат вектора x

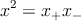(A.2)

равен t². Для времениподобного вектора x, направленного в будущее, x ₊ > 0 и x₋ > 0; аналогично, область прошлого определяется неравенствами x₊ < 0, x₋ < 0, а в области удалённого эти компоненты имеют противоположные знаки (рис. 4).

Координаты x′₊, x′₋ события A относительно наблюдателя 2 (рис. 9) выражаются через его координаты x₊, x₋ относительно наблюдателя 1 формулой (2.7):

(A.3)

При этом x² (A.2) остаётся инвариантным. Эта форма записи преобразования Лоренца эквивалентна (2.8), но выглядит проще.

“Окружность” x² ≡ x ₊x₋ = t² представляет собой гиперболу (рис. 12a); её верхнюю ветвь можно параметрически задать как

Аналогично, правую ветвь “окружности” x² ≡ x ₊x₋ = −r² (рис. 12b) параметрически можно задать как

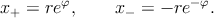Скалярное произведение (3.1) в координатах светового фронта имеет вид

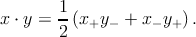(A.4)

Вместо ортонормированного базиса e₀, e₁ введём базис из двух светоподобных векторов

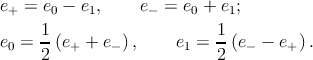(A.5)

Они удовлетворяют свойствам

(A.6)

Любой вектор x можно разложить по этому базису (рис. 21):

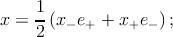(A.7)

компоненты выделяются проецированием:

(A.8)

Если мировая линия второго инерциального наблюдателя образует угол φ с мировой линией первого, то

(A.9)

(рис. 22), и компоненты вектора x во второй системе отсчёта даются формулой (A.3).