Дебанчер-монохроматор инжекционного комплекса ВЭПП-5

А. Петренко (ЦЕРН, 2017)

Здесь приведены расчеты динамики позитронного пучка при инжекции в накопитель-охладитель с дебанчером-монохроматором. Этот ноутбук можно запускать на MS Azure cloud service (файл debuncher.ipynb).

Описание накопителя-охладителя инжекционного комплекса ВЭПП-5:

Схема работы дебанчера (из статьи в ЖЭТФ и проекта c-tau фабрики в ИЯФ, стр. 181):

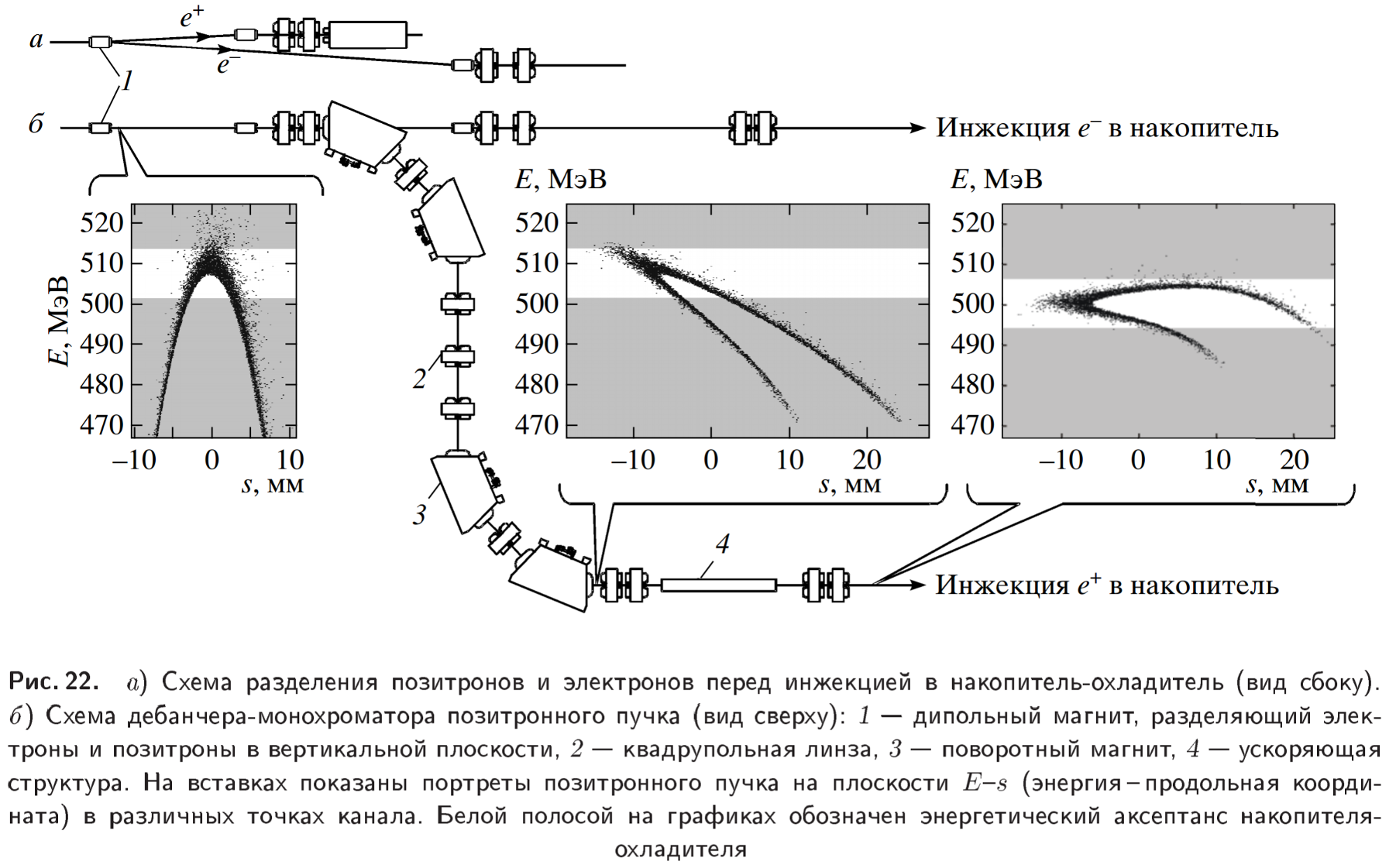
Основные параметры продольной динамики пучка можно определить даже без использования специализированных программ, вроде MAD-X или Elegant.

Энергетически разброс позитронного пучка в конце линейного ускорителя определяются главным образом его длиной, вернее отношением длины пучка к длине волны ускоряющих ВЧ-структур.

Сперва зададим типичные параметры пучка в конце линейного ускорителя:

In [14]:
U_linac = 400 # MV
f_linac = 2856 # MHz -- частота ускоряющих структур

c = 299792458 # m/sec -- скорость света
l_rf_linac = 1e-3*c/f_linac # mm -- длина волны ВЧ в линаке

# Оба этих параметра зависят от параметров исходного электронного сгустка,
# попадающего на мишень для производства позитронов:

sigma_s = 5 # mm -- продольная длина пучка
sigma_p_rnd = 3 # MeV/c --случаная компонента разброса по импульсам
In [15]:
import numpy as np

N = 2000 # количество частиц для моделирования

# Позитронный пучок в конце линейного ускорителя:
s = sigma_s*np.random.normal(size=N)

p = sigma_p_rnd*np.random.normal(size=N) + U_linac * np.cos(2*np.pi*s/l_rf_linac)

Построим это распределение для наглядности.

In [16]:
# Если HoloViews не установлен, надо раскомментировать следующую строку:
#!conda install -y -c ioam holoviews bokeh

import holoviews as hv
#hv.extension('matplotlib')
hv.extension('bokeh')
%output size=120
In [17]:
# matplotlib:
#%opts Points (alpha=0.4, s=5) [show_grid=True]
# Bokeh:
%opts Points (alpha=0.3) [show_grid=True]

E_range = (355,415)
dim_s_E=[ hv.Dimension('s', unit='mm',  range=(-21,31)),
          hv.Dimension('E', unit='MeV', range=E_range) ]

pts = hv.Points((s,p), kdims=dim_s_E)

pts.hist(dimension='E', num_bins=50, bin_range=E_range)
Out[17]:
In [18]:
#hv.help(hv.Points)
#hv.help(hv.extension)

Ускорение позитронного пучка в максимуме ВЧ-волны дает минимально возможный энергетический разброс в конце линака.

Далее в инжекционном канале при параллельном переносе пучка происходит его удлинение за счет зависимости длины траектории позитрона от его энергии:

$$ \Delta l = R_{56} \frac{\Delta p} {p}. $$

Матричный элемент $R_{56}$ выражается через интеграл от дисперсионной функции, деленой на радиус поворота пучка

$$ R_{56} = \int \frac{D(s)ds}{\rho(s)}. $$

В первом диполе ахромата дисперсионная функция растет как $D(s) = [1 − \cos(s/\rho)]\rho$ (что легко получить, решив уравнение на дисперсионную функцию $D'' + k(s)D = 1/\rho$). Далее мы предполагаем, что оба ахромата симметричные, тогда

$$ R_{56} = 4\int\limits_{0}^{\pi\rho/4} [1 − \cos(s/\rho)]ds = \pi\rho - 4\rho\sin(\pi/4) = \rho \left(\pi - 2\sqrt{2}\right). $$
In [19]:
R = 1120 # mm

R56 = R*(np.pi - 2*np.sqrt(2)) # mm

p0 = 390 # MeV/c импульс, на который настроен поворот (интересно его поварьировать)

s = s - R56*(p-p0)/p0 # продольное положение позитронов перед ВЧ-структурой монохроматора

# и снова рисуем портрет пучка:

pts = hv.Points((s,p), kdims=dim_s_E)

pts.hist(dimension='E', num_bins=50, bin_range=E_range)
Out[19]:

Часть пучка будет потеряна в повороте в месте с максимальной дисперсионной функцией. Максимальное значение дисперсионной функции достигается внутри линзы ахромата и равно 57 cм (рис 11 на стр. 12 дипломной работы Ксении Астрелиной). Это значение также можно найти решив уравнение на дисперсию в магните и пустом промежутке от магнита до линзы. Диаметр апертуры вакуумной камеры внутри этой линзы равен 5 см, т.е. максимальное допустимое отклонение частицы от равновесной энергии будет

In [20]:
dp_max = (5/2)/57
print('dp_max * 100 % = {0:.1f} %'.format(dp_max*100))

dp_max * 100 % = 4.4 %
In [21]:
ids = np.where( abs(p - p0) < p0 * dp_max )
p = p[ids]
s = s[ids]
In [22]:
%opts HLine (color='r')

pts = hv.Points((s,p), kdims=dim_s_E)

pts.hist(dimension='E', num_bins=50, bin_range=E_range) * hv.HLine(p0 + p0 * dp_max) * hv.HLine(p0 - p0 * dp_max)
Out[22]:

Далее ВЧ-структура дебанчера-монохроматора уменьшает энергетический разброс пучка перед его инжекцией в накопитель-охладитель:

In [23]:
U_debuncher = 20 # MV
s0 = 0 # mm

l_rf_debuncher = l_rf_linac

def p_after_debuncher(p,s, U=U_debuncher, s0=s0):
    return p + U * np.sin(2*np.pi*(s-s0)/l_rf_debuncher)

p2 = p_after_debuncher(p,s)

# портрет пучка перед инжекцией в накопитель:

pts = hv.Points((s,p2), kdims=dim_s_E)

pts.hist(dimension='E', num_bins=50, bin_range=E_range)
Out[23]:

Интерактивный вариант:

In [24]:
voltages = np.linspace(0,25,6) # MV
phases   = np.linspace(-10,10,5) # mm

#dimensions = ['U', 's0']
dimensions=[ hv.Dimension('U', unit='MV'),
             hv.Dimension('s0', unit='mm') ]
keys = [(U,s0) for U in voltages for s0 in phases]

items = [(k, hv.Points((s,p_after_debuncher(p,s, *k)), kdims=dim_s_E)) for k in keys]

hmap = hv.HoloMap(items, kdims=dimensions)

dp_max_ring = 2.4e-2 # ширина сепаратрисы накопителя-охладителя (как показано ниже)

hmap.hist(dimension='E', num_bins=50, bin_range=E_range) * hv.HLine(p0 + p0 * dp_max_ring) * hv.HLine(p0 - p0 * dp_max_ring)
Out[24]:

Инжекция пучка в накопитель (в работе...)

Unperturbed longitudinal motion is described in terms of energy gain of the ion when it passes the RF-resonator as well as the ion phase with respect to the RF:

$$ E_{n+1} = E_n + e(Z-N_e)V_{\rm{RF}}\cos\phi_n, $$

where $E_n$ is the ion energy and $\phi_n$ is its phase in RF resonator at the $n$-th turn; RF system freqyency $f_{\rm{RF}}$ is some high harmonic $h$ of ion revolution frequency: $$ T_s = \frac{L}{\upsilon_s} = \frac{h}{f_{\rm{RF}}}, $$ where $L$ is the ring perimeter, and $\upsilon_s$ is the reference velocity of the ion, and $T_s$ is the revolution period. If the ion momentum is different from its reference value then the period of revolution $T$ is different from $T_s$: $$ T = \frac{L+\Delta l}{\upsilon_s + \Delta \upsilon} \approx T_s \left ( 1 + \frac{\Delta l}{L} - \frac{\Delta \upsilon}{\upsilon_s} \right ) \approx T_s \left ( 1 + \frac{\Delta l}{L} - \frac{1}{\gamma^2} \frac{\Delta p}{p} \right ). $$ The difference between the length of ion trajectory and the reference orbit length is given by the $M_{56}$ element of the 1-turn transport matrix: $$ \Delta l = M_{56} \frac{\Delta p} {p}. $$ $\Delta T = T - T_s$ in can be written as $$ \Delta T \approx T_s \left ( \frac{M_{56}}{L} - \frac{1}{\gamma^2} \right ) \frac{\Delta p}{p} = T_s \left ( \frac{1}{\gamma_t^2} - \frac{1}{\gamma^2} \right ) \frac{\Delta p}{p} = T_s\eta\frac{\Delta p}{p}. $$ Then the phase is $$ \phi_{n+1} = \phi_n + 2\pi f_{\rm{RF}}(T_s + \Delta T_{n+1}) = \phi_n + 2\pi h + 2\pi h \eta\frac{\Delta p_{n+1}}{p}, $$ $\Delta p$ and $\Delta E$ are related as $$ \frac{\Delta p}{p} = \frac{1}{\beta^2}\frac{\Delta E}{E}, $$ where $\beta = \upsilon/c$.

In [25]:
N_turns = 7000

dE  = np.zeros(N_turns + 1) # energy deviation (eV)
phi = np.zeros(N_turns + 1) # ion phase with respect to RF

eVrf = 10e-3 # MV
#eVrf = 0.8 # MV проектное значение

h = 1 # Гармоника частоты обращения пучка
#h = 64  # проектное значение

mc2 = 0.511 # MeV

gamma_s = p0/mc2

E_s = gamma_s*mc2 # eV
beta_s = np.sqrt(1-1/(gamma_s*gamma_s))

dE[0]  = 2.4e-2*E_s # eV
#dE[0]  = 1.2e-2*E_s*2.2 # eV проектное значение
phi[0] = np.pi/2

gamma_t = 6.0

eta = 1/(gamma_t*gamma_t) - 1/(gamma_s*gamma_s)

for n in range(0, N_turns):
    dE[n+1]  = dE[n] + eVrf*np.cos(phi[n])
    phi[n+1] = phi[n] + (2*np.pi*h*eta/(beta_s*beta_s))*dE[n+1]/E_s
In [26]:
dim_dE    = hv.Dimension('dE/E', unit='%',  range=(-3,+3))
dim_phase = hv.Dimension('phase/pi', range=(0.5-1.1,0.5+1.1))

hv.Points((phi/np.pi, 100*dE/E_s), kdims=[dim_phase,dim_dE]) + \
hv.Points((range(N_turns+1), 100*dE/E_s), kdims=['turn',dim_dE])
Out[26]:

-- т.е. ширина сепратрисы накопителя-охладителя будет 2.4% -- как в проекте.